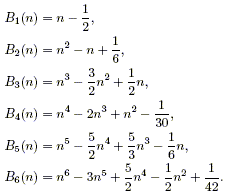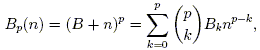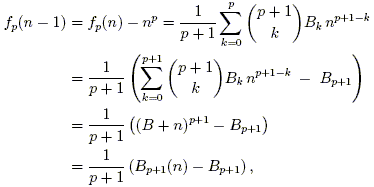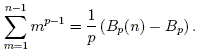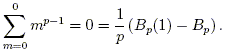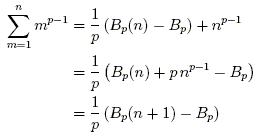We would like to arrive at a computationally simpler formula for the function

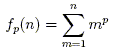(1)

that computes the sum of the first n consecutive like pth powers. Clearly for zeroth powers,

For p = 1, we desire a formula for the sum

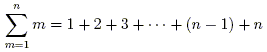
of the first n natural numbers. The first few sums are

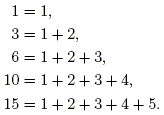
These numbers are known as the triangular numbers because they are the number of dots in the following isosceles right "triangles":

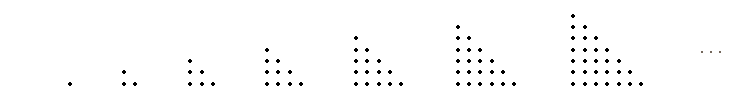
The explicit formula can be obtained by a simple geometric interpetation: The numbers of dots in the triangles are half of the numbers of dots in the following rectangles:

So the nth triangular number is n (n + 1) / 2, and we have the identity

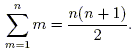
For second powers, there is no obvious geometric interpretation. The sequence begins:

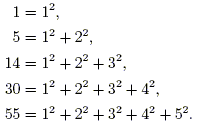
It's not too difficult to guess the correct formula, especially if we suspect that it is given by a polynomial in n, as in the p = 1 case:

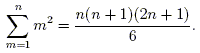
In general, we may suspect that the sum of the first natural numbers raised to the pth power is a polynomial in n of degree p + 1. If this is true, then on a case by case basis it is possible to find this polynomial for a given p (for example, by finding an interpolating polynomial to the first p + 2 points). However, it would be more enlightening to find a closed-form expression for the sum f_p(n).

Without foresight, one approach to this is the following: Record the expressions for several low values of p and look for patterns. By interpolation, we find:

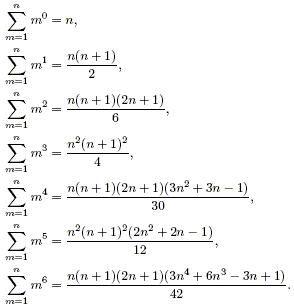
There are no obvious patterns in the larger factors, and the irreducible quartic factor in the formula for p = 6 is somewhat foreboding. Let us change our view of these slightly and look instead at the fully expanded polynomials:

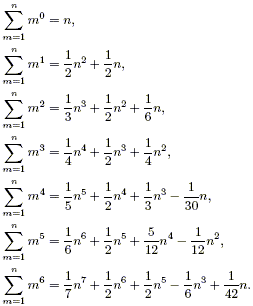
Immediately we notice some patterns: The leading coefficient appears to be 1 / (p + 1), and the coefficient of n^p seems to always be 1 / 2. By clearing away the variables and putting the coefficients in a table to line them up (ignoring the zero constant term 0n⁰ in each case), we see some more structure:

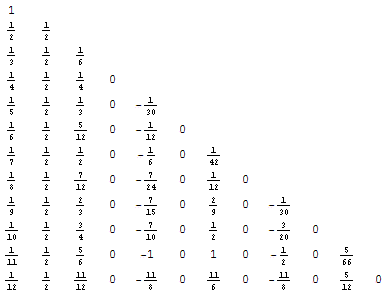
Several columns are simply 0. The coefficient of n^{p – 1} is evidently linear: p / 12. It turns out that the coefficient of n^{p – 3} is given by a cubic in p: –p (p – 1) (p – 2) / 720. In fact, for even k the coefficients of n^{p + 1 – k} are given by a fairly simple polynomial of degree k – 1:

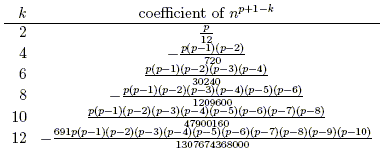
The product can be written more succinctly as , suggesting that we rewrite the above polynomials as binomial coefficients:

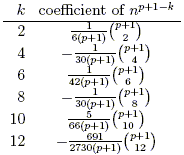
Let B_k be the (signed) constant appearing in the expression for the coefficient of n^{p + 1 – k}. Note that the zero columns in the table of coefficients imply that for odd k > 1, B_k = 0. With the exception of understanding B_k, we have arrived at the following conjectural formula for f_p(n):

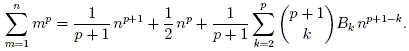
It turns out that the coefficients B_k are simply the Bernoulli numbers:

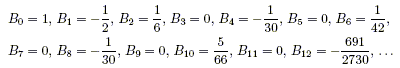
Furthermore, we can even bring the first two terms into the sum if we include a factor of (–1)^k to take care of the fact that B₁ = – 1 / 2 while the coefficient of n^p is 1 / 2:

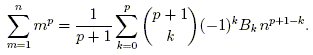(2)

To write the expression (2) more concisely, we now define Bernoulli polynomials and explore some of their properties. For p ≥ 1, let B_p(n) be a polynomial in n of degree p satisfying

(3)

This defines B_p(n) up to its constant term; we define its constant term B_p(0) to be the Bernoulli number B_p. We call B_p(n) the pth Bernoulli polynomial, after Jakob Bernoulli (1654–1705), who discovered them in his attempt to find the general formula for sums of consecutive powers. The first few Bernoulli polynomials are

One property of the Bernoulli polynomials is that

where "B^k" is to be interpreted as B_k. (We do not prove this here but simply take it from the literature.) Then considering f_p(n – 1) rather than f_p(n) puts (2) in this form:

or Bernoulli's form,

(4)

Of course, this wasn't Bernoulli's approach. Bernoulli noted that since the Bernoulli polynomials are defined by (3) up to a constant and

then we must have

for some constant C_p if f_p(n) is a polynomial of degree p + 1. For p ≠ 0 we may redefine f_p(n) as

so that f_p(0) = 0. Putting n = 0 in (3) gives B_p = B_p(1) for p > 1, so for p > 1

This again gives (4).

At last we will actually prove that (4) holds. We do this for every p ≥ 2 by induction on n. (The cases p = 0 and p = 1 were proven in Section I.) Clearly for n = 0

Assume that (4) holds for n. Then

by the definition (3) of B_p(n), so (4) holds for n + 1, completing the induction.

Relevant links:

• Power Sum on MathWorld
• Bernoulli Number on MathWorld
• Bernoulli Polynomial on MathWorld
• Introduction on Bernoulli's Numbers: Bernoulli numbers in sums of powers, power series, and the Riemann zeta function
• The Bernoulli Number Page: a program that computes Bernoulli numbers and some advanced topics