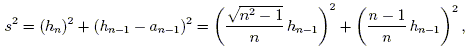As a cube can be created connecting the corresponding vertices of two squares, so can the four-dimensional tesseract be created by connecting corresponding vertices of two cubes, as in the following projection of a tesseract onto the plane.

A tesseract can then be duplicated to create a 5-cube, etc. The hypervolume of an n-dimensional hypercube with side length s is sⁿ because all intersecting line segments intersect perpendicularly. However, the formula for the surface hyperarea of a hypercube is not so intuitive. To find this formula, we need to know how many hyperfaces — (n – 1)-dimensional polyhedra that make up the boundary of the hypercube — each hypercube contains. Moreover, given a hypercube, it would be interesting to know how many vertices, line segments, squares, cubes, tesseracts, etc. it contains. In this direction, let us record some values that can be easily found by counting.

Now we can begin to fill the missing numbers in. Since the tesseract was created by doubling a cube we know it has twice as many vertices as the cube (since in joining two cubes with line segments we do not create any additional vertices). Similarly, the five-cube has twice as many vertices as the tesseract. In general, we can prove by induction that the n-dimensional hypercube has 2ⁿ vertices.

How many edges does a tesseract have? A cube has 12 edges, and the tesseract is composed of two cubes. Therefore the tesseract must have at least 24 edges. However, there are an additional 8 edges that arise as the "connections" between the 8 vertices of each cube. So the tesseract has 2 · 12 + 8 = 32 edges. Similarly, the 5-cube inherits 2 · 32 from its constituent tesseracts, and it also has 16 edges connecting the vertices of the two tesseracts. So the 5-cube has 2 · 32 + 16 = 80 edges. In general, if V_n and E_n are the number of vertices and edges in an n-cube, then E_n = 2 E_{n – 1} + V_{n – 1} = 2 E_{n – 1} + 2^{n – 1}.

What about squares? A tesseract inherits 2 · 6 squares from its constituent cubes. Each edge of the cube forms a new square, however, for a new line segment is drawn at each endpoint. Thus the tesseract has 12 additional squares, formed by the cube's 12 edges. In fact, for every m-cube inside of an n-cube (m ≤ n), we obtain a new (m + 1)-cube inside the (n + 1)-cube. Letting b_{n, m} denote the entry in the nth row and mth column of the table (starting both n and m at 0) then gives

(1)

For all n, b_{n, n} = 1 because each n-cube contains exactly one n-cube. This allows us to complete as much of the table as we like.

We have a recursive formula for b_{n, m}, but perhaps there is an explicit, closed-form expression. Finding such an expression amounts to solving the recurrence relation (1) explicitly. One way to approach this is to handle one column at a time. Fixing m = 1, we can iteratively substitute (1) into itself and work down to an explicit formula:

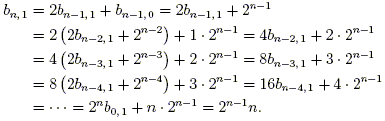
Similarly, for m = 2,

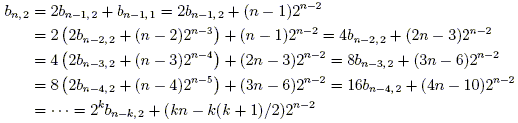
for any 1 ≤ k ≤ n. Here we encounter the triangular numbers — the sequence 1, 3, 6, 10, 15, 21, ..., the kth term of which is the sum of the first k natural numbers. In general, the kth triangular number is given by the binomial coefficient . Letting k = n above, we find

(The above results can be proven more directly by induction.) At this point we might guess that . We prove by induction that this in fact holds, knowing that b_{n, n} = 1 for all n and b_{n, m} = 0 for m > n (which both agree with the expression for b_{n, m}). Assume that

hold for some m < n. Our goal is to show that

holds, for then the recurrence relation and the explicit formula "fill in" the table in the same way. Using equation (1) (and proving the Pascal formula along the way), we have

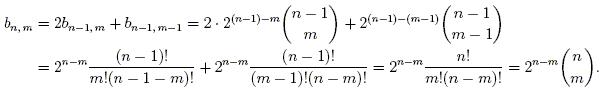
We now return to the question of the surface hyperarea of a regular n-cube of side length s. Since an n-cube has hyperfaces, each of hypervolume s^{n – 1}, the surface hyperarea of a regular n-cube is

An n-simplex is an n-dimensional polytope containing n + 1 vertices, each pair of which is joined by an edge. The 2-simplex is the triangle, and the 3-simplex is the tetrahedron (while the 0- and 1-simplices are the point and the line segment).

Since each vertex is connected to every other vertex, there are edges in an n-simplex. Similarly, any three vertices form a triangle, so there are triangles, etc. The following table lists the number of m-simplices contained in an n-simplex. The entry in the nth row and mth column is

This table is simply Pascal's triangle (left-justified and missing the leftmost column), as its entries are simple binomial coefficients, illustrating a remarkable connection between simplices and the simplex figurate numbers (which comprise the diagonals of Pascal's triangle).

For any n, there is a regular n-simplex, which we can define inductively: There is a point (in four-dimensional space) that is distance s from each of the four vertices of a regular tetrahedron. This point becomes a vertex of the regular pentatope. There is a point (in 5-space) that is distance s from each of the five vertices of the regular pentatope; this point serves as the sixth vertex for the regular 6-simplex, etc.

What is the hypervolume V_n of a regular n-simplex with side length s? It turns out to have a nice formulation in terms of the height h_n of the regular n-simplex (i.e., the distance from a vertex to the center of the opposite hyperface). For the equilateral triangle, V₂ = h₂ · s / 2. The volume of a regular tetrahedron is V₃ = h₃ · V₂ / 3. In general, the hypervolume of an n-dimensional pyramid of height h and base hyperarea A is h · A / n. (This result can be obtained by using calculus.) For regular simplices, this implies that

(2)

However, by breaking up the regular n-simplex into n + 1 congruent (smaller) n-simplices (each of height a_n and the bases of which are the hyperfaces of the n-simplex), we obtain an expression for V_n in terms of the apothem a_n (the radius of the hypersphere inscribed in the n-simplex) and the surface hyperarea S_n = (n + 1) V_{n – 1} of the n-simplex:

Equating this with (2) allows us to solve for h_n:

or a_n = h_n / (n + 1).

The task is now to find an explicit formula for h_n. For the triangle, h₂ = √3 s / 2. The height h₃ of the tetrahedron is found by first knowing the height of the triangle, for the line segment (of length h₃) from a vertex of the tetrahedron to the center of the opposite face makes a right triangle with the slant height segment of the pyramid (of length h₂) and the apothem segment of the base (of length a₂). The Pythagorean theorem then gives that h₂ = s √(2/3). In general,

One way of finding h_n is to substitute this expression back into itself until we obtain h_n in terms of h₂ = √3 s / 2. Another way is to exploit another right triangle:

which gives

Either way, now that we know h_n explicitly, we can use (2) to find V_n. Again, one way of doing this is by iteratively substituting the expression into itself. Another (perhaps less computationally intensive) way is by looking carefully at (2):

(3)

V₁ = s is the hypervolume of a line segment of length s. The expression for V_n will contain n / 2 powers of 2 in the denominator (from the same number of substitutions of (3)); the 1 / n factor in (3) will contribute 1 / n! to V_n; and each √(n + 1) will cancel out the √n term of the previous iteration. Thus

(4)

At this point the surface hyperarea of a regular n-simplex is easy to derive:

(5)

If b_k is the number of k-dimensional polytopes contained in a given n-dimensional polytope, the generalized Euler formula is that

(Notice that b_n = 1, so if n is even then and if n is odd then .)

Relevant links:

• Polytope on MathWorld
• Tesseract on MathWorld
• Hypercube on MathWorld
• Pentatope on MathWorld
• Simplex on MathWorld
• 16-Cell on MathWorld
• Cross Polytope on MathWorld