
| Contents |
Supplements and Links
|
| Objectives: To work with geometric objects that cannot be visualized because they exist in higher dimensions. To find patterns in lower dimensional objects that suggest properties of higher dimensional objects. | Necessary Background: The geometry of Section I is much simpler than that of Section II, but the combinatorics of Section II is considerably simpler than that of Section I. Experience with polyhedra is recommended. |
| Summary: Students derive formulas for the hypervolumes and surface hyperareas of two classes of n-dimensional polytopes which are always regular. Additionally, they count the number of m-dimensional sub-polytopes in each for all m < n. | |
Although we live in a three-dimensional world, it makes mathematical sense to talk about shapes and figures in higher dimensions, even if we cannot ever completely visualize them. Polytopes are the generalizations of polygons and polyhedra to higher dimensions. We'll see two classes of polytopes that are always regular.
Why would we ever think that there may be polytopes in higher dimensions? In fact, they come quite naturally from the following progression. In "zero dimensions" all we can have is a single point; a point is said to be zero-dimensional because there are no coordinates to specify where in the zero dimensional space a particular point is — there's only one! If we add a dimension to a zero-dimensional space, we obtain a straight line. We can think about this in another way: Take a (zero-dimensional) point. Make a copy of that point somewhere else and connect the two points by a line segment. Then we have a one-dimensional line segment.

Given a one-dimensional line, we can copy it and join the endpoints by two more line segments. This gives a two-dimensional square. We can then duplicate the square and join the vertices to obtain a cube.
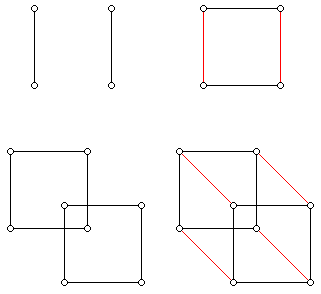
The point, the line segment, the square, and the cube seem to form a fairly nice progression. What happens if we try to duplicate a cube in this way? Well, we are already working in three dimensions, so we cannot visualize what happens exactly. Rather, we can project the cube and its copy back into three-dimensional space (just as, in order to represent to squares, we have projected, or flattened, down the cube in order to represent it on a two-dimensional page). What we obtain when we join the vertices of the two cubes is a called a tesseract:
The above picture is a projection of a tesseract into the two-dimensional plane. (If you want to get a better feel for the geometry, you can make two cubes out of pipe cleaners or long matches and connect the vertices.)
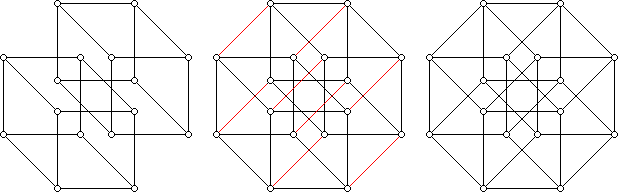
And we need not stop here. A tesseract is the fourth-dimensional analogue of a cube. In general, the n-dimensional cubes are called hypercubes or, to specify the dimension, n-cubes. We can take two tesseracts and join their vertices with additional line segments to obtain a five-dimensional hypercube, etc. It turns out that all of these n-dimensional hypercubes are regular — they are composed of congruent (n – 1)-dimensional hypercubes and their vertices are identical.
As a polygon has an area and a polyhedron has a volume, a four-dimensional polytope has a hypervolume — a four-dimensional measurement of the "content" of the polytope. In general, an n-dimensional polytope is said to have a hypervolume, which is always the n-dimensional content measurement. What is the hypervolume of an n-dimensional hypercube of side length s?
We can also ask about the surface "hyperarea" of a polytope. As the boundary of a polygon is composed of line segments and the boundary of a polyhedron is composed of polygons, the boundary of an n-dimensional polytope is composed of (n – 1)-dimensional polytopes, which we could call the hyperfaces of the polytope. The surface hyperarea is the sum of the hypervolumes of the (n – 1)-dimensional hyperfaces. By examining some low dimensional cases, make a conjecture about how many (n – 1)-dimensional hypercubes are contained in an n-dimensional hypercube. (All of these are hyperfaces of the hypercube).
How many vertices are there in an n-dimensional hypercube? Prove your answer.
The following table lists some n-dimensional hypercubes and the number of various lower-dimensional hypercubes that each contains. Fill in the blank entries.
| hypercube | vertices | edges | squares | cubes | tesseracts |
| 0 – point | 1 | 0 | 0 | 0 | 0 |
| 1 – line segment | 2 | 1 | 0 | 0 | 0 |
| 2 – square | 4 | 4 | 1 | 0 | 0 |
| 3 – cube | 1 | 0 | |||
| 4 – tesseract | 1 |
What is bn, m in terms of n and m?
What is the surface hyperarea of an n-dimensional hypercube?
Another class of polytopes which are regular for all n generalize from the triangle and the tetrahedron. (We can even consider the zero- and one-dimensional cases to be a point and a line segment again.) Members of this class are called n-dimensional simplices or n-simplices. The 4-simplex is called a pentatope, for it has five vertices, each one connected to every other. How many vertices does an n-simplex have?
Fill in the blank entries in the following table.
| simplex | vertices | edges | triangles | tetrahedrons | pentatopes |
| 0 – point | 1 | 0 | 0 | 0 | 0 |
| 1 – line segment | 2 | 1 | 0 | 0 | 0 |
| 2 – triangle | 3 | 3 | 1 | 0 | 0 |
| 3 – tetrahedron | 4 | 1 | 0 | ||
| 4 – pentatope | 5 | 1 |
The height hn of a regular n-simplex is the distance from a vertex of the n-simplex to the center of the opposite hyperface. What is hn in terms of the side length s? (It might help to find a relationship between hn and the apothem an, the radius of the inscribed n-dimensional hypersphere. (In other words, an is the distance from the center of the n-simplex to the center of a hyperface.))
What is the hypervolume of a regular n-simplex of side length s?
Based on the values for hypercubes and n-simplices, try to guess the generalization of Euler's formula to n dimensions.
Relevant links: