Contents

• I. Linear and Quadratic Equations
• II. The Cubic Equation
• References

What are the solutions for the variable x in the polynomial equation

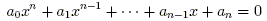
of degree n, given the (real or complex) coefficients a₀, ..., a_n? For n = 1 the equation is

This equation is linear in x, and its solution is

(1)

For the degree n = 2, we obtain a quadratic equation:

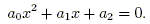
The quadratic formula tells us the solutions of this equation. To derive the quadratic formula, we "complete the square" as follows. Multiply both sides by 4a₀, and then add a₁² to both sides to obtain

The left side of this equation is now a square, so it becomes

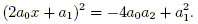
Next, raise both sides to the power 1 / 2 and solve for x. The quadratic formula is

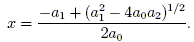(2)

Here, the exponent 1 / 2 means to take both square roots (as complex numbers); each gives rise to a solution. The quadratic formula is frequently written in the following form, as "plus or minus" a square root sign:

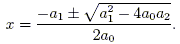
While the latter form is perhaps more explicit, the former lends itself better to generalization. In the case of the cubic equation below, we will need to extract cube roots, so our notation will be more like that of (2).

The cubic equation

is significantly more difficult to solve than the quadratic equation, and its general solution was not found until the sixteenth century. The cubic formula is more complicated than the quadratic formula and cannot reasonably be written without a change of variables.

Analogously to the quadratic case, we "complete the cube" by first multiplying the equation by 27a₀². Adding and subtracting a certain quantity lets us write

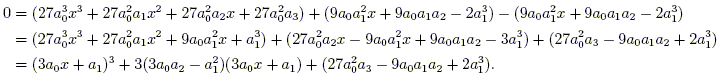
We simplify this by defining

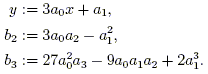
We now seek a solution for y in

or

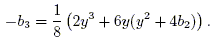
In this form, the identity

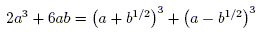
with a = y and b = y² + 4b₂ implies that

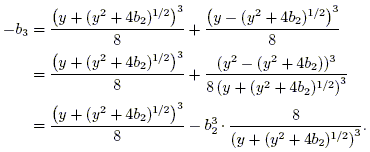
Now define the variable

We have

or

This equation is quadratic in z³, so using the quadratic formula (2) we find

Defining the constant c by

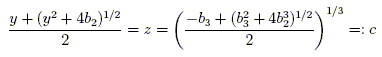
gives

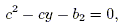
or

Re-introducing x from the definition of y gives the final expression

(3)

for the three solutions of the cubic equation, obtained by taking the three cube roots of c³. (It appears that we might get six distinct solutions, since we also have a choice of one of two square roots in the definition of c, but one checks that in fact selecting either value gives the same solution for x.) In the case that c³ is real, we can write this somewhat more explicitly by selecting as c the real cube root and letting ζ₃ be a cube root of unity (i.e. 1, (–1 + i√3)/2, or (–1 – i√3)/2). The cubic formula is then

Relevant links:

• Cubic Formula on MathWorld
• Quartic Equation on MathWorld
• Quintic Equation on MathWorld