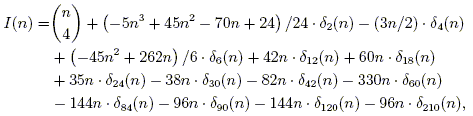Below is a table and diagram summarizing the variables used in the explanation. Angles are measured in degrees throughout so that this information will be accessible to students who have not worked in radians. The results can be converted to radians using the conversion 180° = π radians.

	A	area enclosed by polygon
	a	apothem (radius of inscribed circle)
	dk	length of kth diagonal
	d	diameter of circumscribed circle
	m	length of median
	n	number of sides
	p	perimeter
	r	radius of circumscribed circle
	s	length of side
	α	smallest angle formed by a diagonal and a side
	θ	angle formed by consecutive sides
	φ	angle formed by consecutive radii (the central angle)

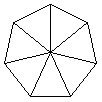
The perimeter of a regular n-gon with side length s is p = ns. To find the area, we divide the polygon into n congruent triangles by drawing segments from the center to each vertex, as illustrated for the septagon to the right.

The sum of the central angles is 360° since it represents the interior angle of a circle, so φ = 360/n. The area of each triangle is as/2 and there are n triangles, so A = nas/2 is the area of a regular n-gon with side length s and apothem a. This can be simplified to A = ap/2; this formulation provides a basis for generalization to higher dimensions.

The sum of the interior angles of a triangle equals 180°, so 180 = φ + θ; this gives

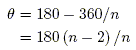
after substition for φ. Then the sum of the angles of a (regular) polygon is nθ = 180(n – 2).

In the same triangles used above, the law of sines gives

which we can use to find s in terms of the radius r:

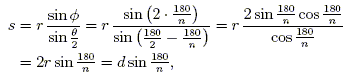(1)

where d = 2r is the diameter of the circumscribed circle.

By the Pythagorean theorem,

Substituting from equation (1) gives

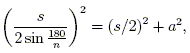
which we solve for a to obtain

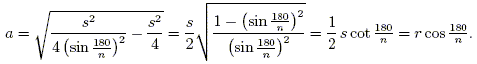(2)

(This expression can also be found using the law of sines as for (1).) Substituting this into A = nas/2 for a, we find

(3)

When n is odd, m = r + a. Substituting for a and r yields

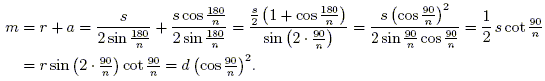(4)

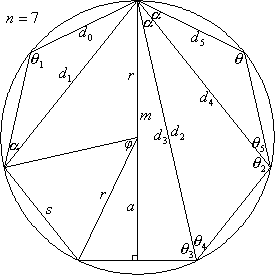
Finally we will find the lengths of diagonals in a regular polygon. From a given vertex, draw a segment to each of the n – 1 other vertices, and call the lengths of these segments (in order) d₁, d₂, ..., d_{n – 1}, as illustrated below.

d₁ = d_{n – 1} = s because these lengths correspond to sides of the polygon. Define α as the angle between any two consecutive segments d_i and d_{i + 1}. All these angles are the same because they subtend the same arc length of the circle. Specifically, by the angle in circle theorems, α = φ/2 = 180/n. (This can also be obtained from the equation 180 = θ + 2α, which is the sum of the angles in the triangle formed by two consecutive sides and a d₂ diagonal.)

For k = 2, 3, ..., n – 2, let θ_k be the angle opposite of diagonal k in the triangle formed a side, diagonal k, and diagonal k – 1. Then θ₂ = θ and θ_{n – 1} = α, and in general

By the law of sines in the kth triangle,

Solving for d_k, we find

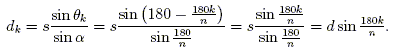(5)

To summarize, the following equations hold for regular polygons (n ≥ 3).

A diagonal is defined to be a line connecting two nonconsecutive vertices of a polygon. All polygons with the same number of sides have the same number of diagonals, so the number of diagonals of a regular n-gon will be the number of diagonals of any polygon with n sides.

To derive an expression for the number D(n) of diagonals in an n-gon, we will count the total number of line segments that connect two vertices, including the sides, and then subtract n from the result to take care of the sides. Starting at a given vertex, there are n – 1 lines to be drawn to other vertices. The next vertex already has a line drawn to the first vertex, so only n – 2 line segments can be drawn. The third vertex can be connected to only n – 3 vertices, and so on, until we reach the last vertex, which already has a line segment to every other vertex. The total number of line segments drawn is

Subtracting n gives a count of

(6)

diagonals.

If V is the number of intersection points ("vertices"), E is the number of segments ("edges"), and F is the number of regions ("faces") including the region that is the exterior of the polygon, then Euler's formula is

Using Euler's formula, then, if we know the number of intersection points and the number of segments, then the number of regions is F = E – V + 2 (or E – V + 1 if we only want to count interior regions).

Let

From Poonen and Rubinstein's paper, the number of interior intersections made by the diagonals of a regular n-gon is

and the number of regions is

For a regular 24-sided polygon, these formulas tell us that the diagonals make 7321 interior intersections, 9024 regions, and 16344 segments.

B. Poonen and M. Rubinstein, The Number of Intersection Points Made by the Diagonals of a Regular Polygon, SIAM J. Discrete Math., v.11 (1998), p. 135–156.

Relevant links:

• Regular Polygon on MathWorld