This calculator computes various combinatorial and geometric values of a regular polygon with its diagonals drawn in. Input the number of sides n (greater than 2) and the radius of the circumscribed circle. See below for a more detailed description of the calculator.

A regular -gon with radius of circumscribed circle r = has the properties:

Combinatorial Quantities:
Diagonals:
Intersections:
Regions:
Segments:
Geometric Values:
Angle θ = °
radians
Side length s =
Perimeter p =
Apothem a =
Median length m = r + a =
Area A =

The calculator gives the following quantities (which are discussed in the Regular Polygons Project):
Diagonals — the number of proper diagonals in a regular polygon (i.e., excluding the n sides)
Intersections — the number of intersections (including the n vertices) of all the diagonals of a regular polygon
Regions — the number of regions into which the diagonals cut the interior of the polygon
Segments — the number of segments (including the n sides of the polygon) that the diagonals cut each other into

Formulas for the numbers of intersections and regions are taken from:
B. Poonen and M. Rubinstein, The Number of Intersection Points Made by the Diagonals of a Regular Polygon, SIAM J. Discrete Math., v.11 (1998), p. 135–156.

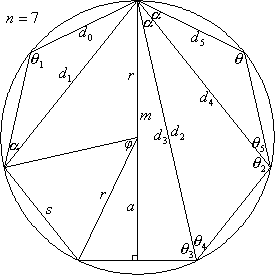
The following regular septagon illustrates the geometric values. Equations relating these values are given at Regular Polygons.