The axioms of mathematics allow us to use a technique called induction in proofs of mathematical statements. This technique often enables us to prove a statement about infinitely many things. For example, suppose we want to prove that every natural number (1, 2 = 1 + 1, 3 = 1 + 1 + 1, ...) is greater than 0. This statement is somewhat obvious to us because of our extensive experience with the system of natural numbers, but we can still ask for a rigorous proof.

An induction argument consists of two parts:

  1. The base case.
  2. The inductive step.

The base case is the "lowest" case that we are interested in, and we prove it for its own sake. In the example of proving that every natural number is greater than 0, the base case is proving that 1 > 0, since 1 is the lowest case that we are interested in. Well, it is an axiom of the real number system that 1 > 0, so there is nothing to prove. (You might argue that the statement "2 > 0" does not require proof either. However, this is not an axiom of the real numbers; rather, it is derived from the axioms.)

The inductive step is where the "induction" happens, and it is usually more difficult than the base case. In the inductive step, we assume that the statement we are trying to prove does hold for some number k. Then, assuming that it holds for k, we show that it also holds for k + 1. If our base case is 1, then by the inductive step, the statement also holds for 2. Since it holds for 2, the inductive step implies that it also holds for 3. Since it holds for 3, it also holds for 4, etc. So simply by showing that the base case holds and that we can proceed inductively on all numbers, we have set up a domino effect that proves our statement for infinitely many numbers.

In the example above, the inductive step is the following: Show that if k > 0, then k + 1 > 0. We use the axiom that if a > b and c > 0, then a + c > b + c. With a = k, b = 0, c = 1, this gives

k + 1 > 1 > 0,

completing the proof.

For a slightly less trivial example, let's prove that the sum of the first n natural numbers is

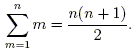(1)

Clearly for n = 1 we have

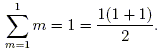
For the inductive step, assume that equation (1) holds for n. We wish to show that it also holds for n + 1. We have

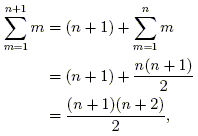
which is what was to be shown. By the principle of mathematical induction, equation (1) holds for all natural numbers n.